Cách tìm tâm, bán kính mặt cầu ngoại tiếp cực hay
Bài giảng: Các dạng bài toán liên quan đến mặt cầu – Cô Nguyễn Phương Anh (Giáo viên VietJack)
A. Tự luận
Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA = 2a và vuông góc với (ABCD). Tính thể tích của khối cầu ngoại tiếp khối chóp S.ABCD.
Bạn đang xem: Tính bán kính mặt cầu ngoại tiếp
Bạn đang xem: tính bán kính mặt cầu ngoại tiếp hình chóp
Hướng dẫn:
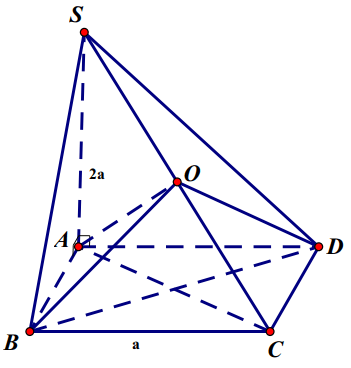
Gọi O là trung điểm của SC
Xét các vuông tại A ∆SAC; ∆SAD; ∆SAB có:
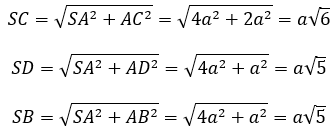
Ta có:
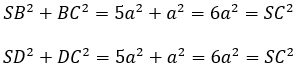
⇒ ∆SBC; ∆SCD vuông tại C
Hình chóp S.ABCD có:
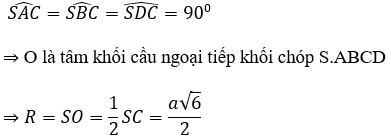
Thể tích khối cầu là:
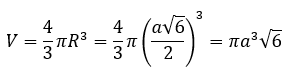
Bài 2: Cho tứ diện ABCD có DA = 5a và vuông góc với (ABC), ∆ABC vuông tại B và AB = 3a, BC = 4a. Diện tích của mặt cầu ngoại tiếp tứ diện ABCD là:
Hướng dẫn:
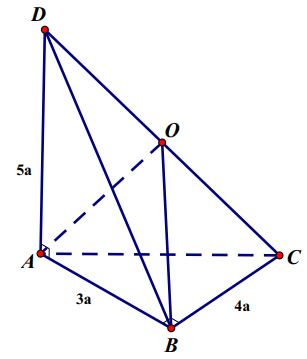
Xét các vuông tại A ∆BAC; ∆DAB; ∆DAC có:
AC2 = BC2 + AB2 = 16a2 + 9a2 = 25a2
DB2 = DA2 + AB2 = 25a2 + 9a2 = 34a2
DC2 = DA2 + AC2 = 25a2 + 25a2 = 50a2
Xét ∆DBC có:
DB2 + BC2 = 34a2 + 16a2 = 50a2 = DC2
⇒ ∆DBC vuông tại B
Gọi O là trung điểm của CD
∆DAC vuông tại A có AO là trung tuyến
⇒ OA = OC = OD = CD/2 (1)
∆DBC vuông tại B có BO là trung tuyến
⇒ OB = OC = OD = CD/2 (2)
Từ (1) và (2) ta có:
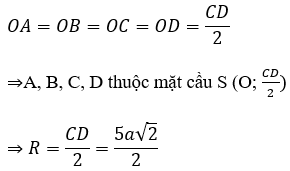
Diện tích của mặt cầu ngoại tiếp tứ diện ABCD là:
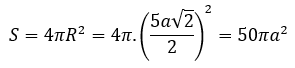
Bài 3: Cho hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 30º. Tính thể tích mặt cầu ngoại tiếp hình chóp
Hướng dẫn:
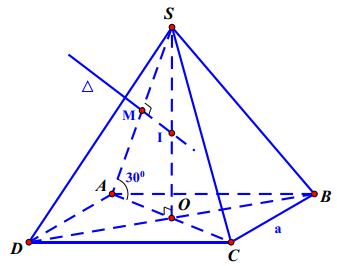
Gọi O là tâm đáy ABCD
Hình chóp S.ABCD đều nên SO ⊥ (ABCD)
OA là hình chiếu vuông góc của SA lên (ABCD)
⇒ Góc giữa cạnh bên SA và đáy là góc ∠(SAO)=30º
Gọi M là trung điểm của SA. Trung trực của SA cắt SO tại I
⇒ I là tâm mặt cầu ngoại tiếp hình chóp.
ABCD là hình vuông cạnh a, O là tâm
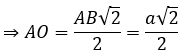
Ta có: ∆SMI ~ ∆SOA (g.g)
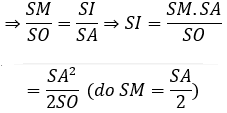
Xét ∆SOA vuông tại O, ∠(SAO) = 30º có:
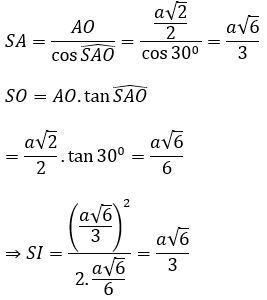
Thể tích mặt cầu là:
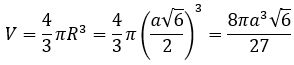
Bài 4: Cho lăng trụ tam giác đều có đáy là tam giác đều có cạnh đáy bằng 2√3, cạnh bên bằng √5. Tính thể tích mặt cầu ngoại tiếp lăng trụ
Hướng dẫn:
Áp dụng công thức giải nhanh:
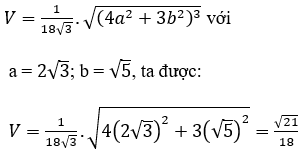
Công thức tính nhanh: Cho lăng trụ tam giác đều có đáy là tam giác đều cạnh a, cạnh bên bằng b.
Bán kính mặt cầu ngoại tiếp:
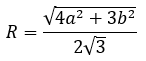
Thể tích khối cầu ngoại tiếp:
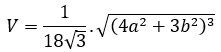
Chứng minh:
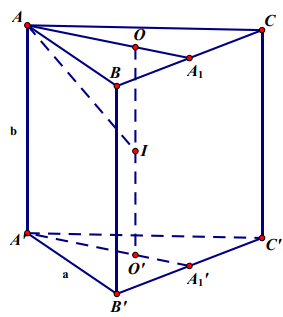
Gọi O, O’ là tâm của ∆ABC và ∆A’ B’ C’ là OO’ là trục của đường tròn ngoại tiếp ∆ABC và ∆A’ B’ C’.
Xem thêm: 10 Cách Khắc Phục Lỗi Không Vào Được Các Trang Web Trên Google Chrome
Gọi I là trung điểm của OO’ thì IA = IB = IC = IA’ = IB’ = IC’ hay I là tâm mặt cầu ngoại tiếp hình trụ. Bán kính mặt cầu là R = IA.
∆AOI vuông có:
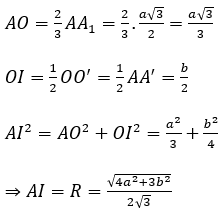
Thể tích khối cầu ngoại tiếp lăng trụ:
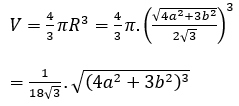
Bài 5: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2 và cạnh bên bằng 2√3. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC
Hướng dẫn:
Áp dụng công thức giải nhanh:
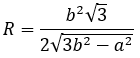
Trong đó, a = 2; b=2√3 ta được:
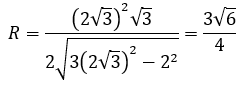
Công thức tính nhanh: Cho hính chóp tam giác đều có đáy là tam giác đều cạnh a, cạnh bên bằng b.
Bán kính mặt cầu ngoại tiếp:
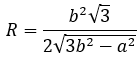
Thể tích khối cầu ngoại tiếp:
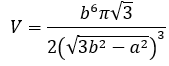
Chứng minh:
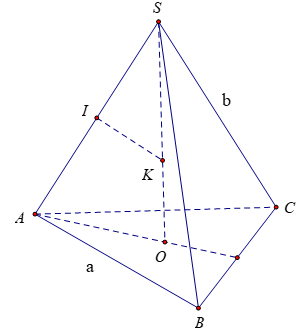
Gọi O là hình chiếu của S lên mặt phẳng (ABC) thì O là tâm của đường tròn ngoại tiếp ∆ABC đều cạnh a.
Mặt phẳng trung trực của SA cắt SA tại I và cắt SO tại K
Khi đó SK = KB = KC hay K là tâm của mặt cầu ngoại tiếp hình chóp S.ABC
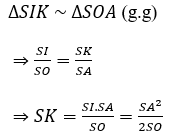
Tam giác SOA vuông tại O
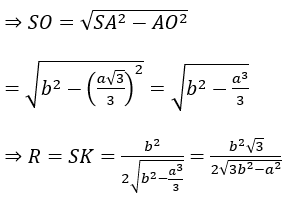
B. Trắc nghiệm
Bài 1: Cho hình chóp S.ABCD có đáy là hình thang cân ABCD với AB=2a, BC=CD=DA=a và SA (ABCD). Một mặt phẳng qua A vuông góc với SB và cắt AB, SC, SD lần lượt tại M, N, P. Tính đường kính khối cầu ngoại tiếp khối ABCDMNP.
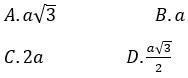
Bài 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA = a.Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
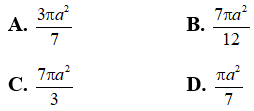
Bài 3: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB=a. Cạnh bên SA vuông góc mp(ABC) và SC hợp với đáy một góc bằng 60º. Gọi (S) là mặt cầu ngoại tiếp hình chóp S.ABC. Thể tích của khối cầu tạo nên bởi mặt cầu (S) bằng:
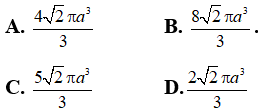
Bài 4: Cho hình lăng trụ tam giác đều ABC. A’B’C’ có tất cà các cạnh đều bằng a.Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
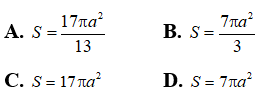
Bài 5: Cho tứ diện S.ABC, đáy ABC là tam giác vuông tại B với AB = 3, BC = 4. Hai mặt bên (SAB) và (SAC) cùng vuông góc với (ABC) và SC hợp với (ABC) góc 45º. Thể tích hình cầu ngoại tiếp S.ABC là:
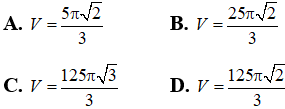
Bài 6: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.

Bài 7: Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Bán kính mặt cầu ngoại tiếp của khối lập phương ABCD. A’B’C’D’ bằng
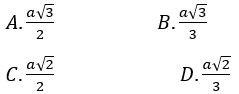
Bài 8: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD theo a.
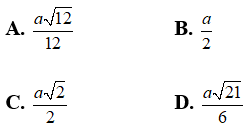
Bài tập tìm tâm, bán kính mặt cầu ngoại tiếp (phần 2)
Bài 1: Cạnh bên của một hình chóp tam giác đều bằng a tạo với mặt đáy một góc 30º. Diện tích mặt cầu ngoại tiếp hình chóp là :

Bài 2: Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a . Mặt phẳng (AB’C’) tạo với mặt phẳng (A’B’C’) một góc 60º và G là trọng tâm ∆ABC . Diện tích mặt cầu ngoại tiếp khối chóp G.A’B’C’ bằng:

Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ∠(BAD) =60º. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm M của cạnh AB. Biết SD = a√3 Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABD.
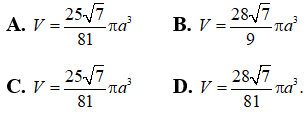
Bài 4: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD. Tính bán kính R của khối cầu ngoại tiếp hình chóp S.CMN.
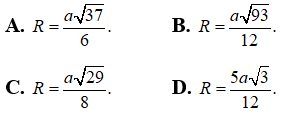
Bài 5: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là trung điểm H của cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60°. Gọi G là trọng tâm tam giác SAC, R là bán kính mặt cầu có tâm G và tiếp xúc với mặt phẳng (ABC). Đẳng thức nào sau đây sai?
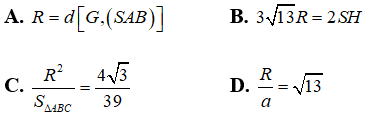
Bài 6: Cho hình lập phương có cạnh bằng a. Gọi R1 và R2 lần lượt là bán kính mặt cầu nội tiếp và ngoại tiếp hình lập phương. Tính tỉ số R1/R2.
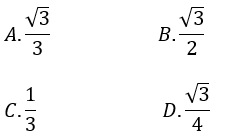
Bài 7: Cho khối chóp S.ABC có đáy ABC vuông tại A, AB = a, AC = 2a, SA = SB = SC và mặt bên (SAB) hợp với đáy (ABC) một góc 60º. Diện tích mặt cầu ngoại tiếp hình chóp S.ABC là:
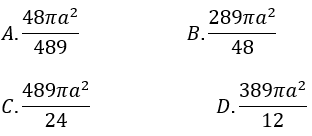
Giới thiệu kênh Youtube VietJack
Tham khảo: Kiến thức Nhiệt lượng là gì? Đơn vị, công thức tính nhiệt lượng









