Bài toán tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của biểu thức cũng là dạng toán chứng minh biểu thức luôn dương hoặc luôn âm hoặc lớn hơn hay nhỏ hơn 1 số nào đó.
Bạn đang xem: Cách tìm giá trị lớn nhất
Cụ thể cách tìm giá trị lớn nhất (GTLN) hay giá trị nhỏ nhất (GTNN) của biểu thức như thế nào? Chúng ta sẽ tìm hiểu qua bài viết dưới đây để 1ua đó vận dụng giải một số bài tập tìm GTLN, GTNN của biểu thức.
I. Cách tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của biểu thức
• Cho một biểu thức A, ta nói rằng số k là GTNN của A nếu ta chứng minh được 2 điều kiện:
i) A ≥ k với mọi giá trị của biến đối với biểu thức A
ii) Đồng thời, ta tìm được các giá trị của biến cụ thể của A để khi thay vào, A nhận giá trị k.
• Tương tự, cho biểu thức B, ta nói rằng số h là GTLN của B nếu ta chứng minh được 2 điều kiện:
i) B ≤ h với mọi giá trị của biến đối với biểu thức B.
ii) Đồng thời, ta tìm được các giá trị của biến cụ thể của B để khi thay vào, B nhận giá trị h.
* Lưu ý: Khi làm bài toán tìm GTLN và GTNN học sinh thường phạm phải hai sai lầm sau:
1) Khi chứng minh được i), học sinh vội kết luận mà quên kiểm tra điều kiện ii)
2) Đã hoàn tất được i) và ii), tuy nhiên, học sinh lại quên đối chiếu điều kiện ràng buộc của biến.
Hiểu đơn giản, bài toán yêu cầu xét trên một tập số nào đó của biến (tức là thêm các yếu tố ràng buộc) mà học sinh không để ý rằng giá trị biến tìm được ở bước ii) lại nằm ngoài tập cho trước đó.

* Ví dụ 1: Tìm giá trị nhỏ nhất của biểu thức: A = (x2 + 1)2 - 3
Giả sử lời giải như sau:
Vì (x2 + 1)2 ≥ 0 nên (x2 + 1)2 - 3 ≥ -3 ⇔ A ≥ -3
Kết luận giá trị nhỏ nhất của A bằng -3.
→ Kết luận về GTNN như thế là mắc phải sai lầm 1) ở trên, tức là quên kiểm tra điều kiện ii).
Thực ra để cho A bằng 4, ta phải có (x2 + 1)2 = 0 , nhưng điều này không thể xảy ra được với mọi giá trị của biến x.
* Ví dụ 2: Với x là số nguyên không âm, tìm giá trị nhỏ nhất của biểu thức: A = (x + 2)2 - 5.
Xem thêm: Những Cách Chống Trộm Xe Máy An Toàn Khiến Trộm 'Khóc Thét'
Giả sử lời giải như sau:
Vì (x + 2)2 ≥ 0 nên (x + 2)2 - 5 ≥ - 5 ⇔ A ≥ - 5
Dấu "=" xảy ra khi và chỉ khi (x + 2)2 = 0 ⇔ x + 2 = 0 ⇔ x = -2
Kết luận GTNN của A = -5 khi x = -2.
→ Kết luận như vậy mắc phải sai lầm 2) ở trên, vì bài toán cho x là số nguyên không âm nên x sẽ không nhận giá trị x = -2 để min(A) = -5 được.
Như vậy các em cần lưu ý khi tìm GTLN và GTNN của một biểu thức (A) thì biểu thức (A) đạt GTLN hay GTNN đó khi biến (x) nhận giá trị bằng bao nhiêu, giá trị này có thỏa ràng buộc biến của bài toán hay không sau đó mới kết luận.
II. Bài tập tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của biểu thức
• Dạng 1: Tìm GTNN, GTLN của biểu thức có dạng tam thức bậc 2
Phương pháp: Đối với dạng tam thức bậc hai ta đưa biểu thức đã cho về dạng bình phương một tổng (hoặc hiệu) cộng (hoặc trừ) đi một số tự do, dạng:
d - (a ± b)2 ≤ d Ta tìm được giá trị lớn nhất.(a ± b)2 ± c ≥ ± c Ta tìm được giá trị nhỏ nhất.* Bài tập 1: Tìm giá trị nhỏ nhất của biểu thức sau: A = (x - 3)2 + 5
> Lời giải:
- Vì (x - 3)2 ≥ 0 ⇔ (x - 3)2 + 5 ≥ 5 ⇔ A ≥ 5.
Vậy giá trị nhỏ nhất của biểu thức là A = 5 xảy ra khi x - 3 = 0 ⇔ x = 3.
Kết luận: GTNN của A là 5 đạt được khi x = 3.
* Bài tập 2: Tìm giá trị nhỏ nhất của biểu thức sau: A = 2x2 - 8x + 3
> Lời giải:
- Ta có: A = 2x2 - 8x + 3 = 2x2 - 8x + 8 - 5
⇔ A = 2x2 - 8x + 8 - 5
⇔ A = 2(x2 - 4x + 4) - 5
⇔ A = 2(x - 2)2 - 5
Vì (x - 2)2 ≥ 0 ⇒ 2(x - 2)2 ≥ 0 ⇒ 2(x - 2)2 - 5 ≥ -5
Dấu "=" xảy ra khi (x - 2)2 = 0 ⇔ x - 2 = 0 ⇔ x = 2.
Kết luận: GTNN của A là 5 đạt được khi x = 2.
* Bài tập 3: Tìm GTNN của biểu thức: A = 2x2 - 6x
> Lời giải:
- Ta có: A = 2x2 - 6x
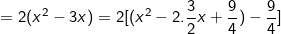
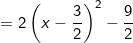
Vì
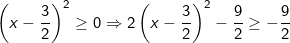
Dấu "=" xảy ra khi
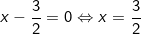
Vậy GTNN của A bằng -9/2 đạt được khi x = 3/2
* Bài tập 4: Tìm giá trị lớn nhất (GTLN) của biểu thức: B = 2 + 4x - x2
> Lời giải:
- Ta có: B = 2 + 4x - x2 = 6 - 4 + 4x - x2
= 6 - (4 - 4x + x2) = 6 - (2 - x)2
Vì (2 - x)2 ≥ 0
⇒ -(2 - x)2 ≤ 0 (đổi dấu đổi chiều biểu thức)
⇒ 6 - (2 - x)2 ≤ 6 (cộng hai vế với 6)
Vậy GTLN của biểu thức B bằng 6 đạt được khi (2 - x)2 = 0 ⇒ x = 2.
* Bài tập 5: Tìm giá trị lớn nhất (GTLN) của biểu thức: C = 2x - x2
> Lời giải:
- Ta có: C = 2x - x2 = -x2 + 2x - 1 + 1
= 1 - (x2 - 2x + 1) = 1 - (x - 1)2
Vì (x - 1)2 ≥ 0
⇒ -(x - 1)2 ≤ 0 (đổi dấu đổi chiều biểu thức)
⇒ 1 - (x - 1)2 ≤ 1 (cộng hai vế với 1)
Vậy GTLN của biểu thức C bằng 1 đạt được khi (x - 1)2 = 0 ⇒ x = 1
• Dạng 2: Tìm GTNN, GTLN của biểu thức có chứa dấu trị tuyệt đối
Phương pháp: Đối với dạng tìm GTLN, GTNN này ta có hai cách làm sau:
+) Cách 1: Dựa vào tính chất |x| ≥ 0. Ta biến đổi biểu thức A đã cho về dạng A ≥ a (với a là số đã biết) để suy ra giá trị nhỏ nhất của A là a hoặc biến đổi về dạng A ≤ b (với b là số đã biết) từ đó suy ra giá trị lớn nhất của A là b.
+) Cách 2: Dựa vào biểu thức chứa hai hạng tử là hai biểu thức trong dấu giá trị tuyệt đối. Ta sẽ sử dụng tính chất:
∀x, y ∈ Q ta có:
|x + y| ≤ |x| + |y| Dấu "=" xảy ra khi x.y ≥ 0|x - y| ≤ |x| - |y|* Bài tập 6: Tìm giá trị nhỏ nhất của biểu thức: A = (2x - 1)2 - 6|2x - 1| + 10









