Đường tròn là trong số những hình học tập khó với nhiều dạng bài bác tập khác nhau. Để hoàn toàn có thể hiểu được đầy đủ về hình học này cần khẳng định được lý thuyết tương tự như bài tập về đường kính cùng dây của đường tròn.
Bạn đang xem: Đường kính và dây của đường tròn
bởi vì vậy hãy cùng https://pgdngochoi.edu.vn/ theo dõi bài xích giảng sau cùng với những bài tập phổ cập về mảng kiến thức và kỹ năng này để chúng ta học sinh hoàn toàn có thể áp dụng.I. Kim chỉ nan về 2 lần bán kính và dây của mặt đường tròn:
1. Cung với dây cung của con đường tròn:
Cho con đường tròn tất cả tâm là O và có 2 điểm khác nhau là A cùng B nằm trên phố tròn thì 2 điểm đó sẽ phân chia đường tròn làm cho 2 phần. Đối cùng với 2 phần này, từng phần vẫn được coi là một cung.
Trong đó:
2 điểm A và B được hotline là 2 mút của cung.Đoạn thẳng nối sát 2 mút của cung được hotline là dây cung (dây).Dây cung trải qua tâm của con đường tròn được gọi là mặt đường kính.Ngoài ra trong một mặt đường tròn còn có mối tình dục giữa 2 lần bán kính và dây cung như sau: Đường kính đã dài gấp hai bán kính.
2. đối chiếu giữa độ dài dây cung và con đường kính:
Định lý 1:
Trong tất cả các dây cung của đường tròn, dây cung lớn số 1 là đường kính.Xét một đường tròn tâm O, bán kính R, (O , R) ta có:
A ∈ O, B ∈ O ⇒ AB ≤ 2R
So sánh thân độ nhiều năm dây cung và 2 lần bán kính của mặt đường tròn trọng tâm O
Chứng minh:
Trường đúng theo 1:Nếu đường kính của con đường tròn là dây AB thì AB = 2R
Trường thích hợp 2:Nếu đường kính của mặt đường tròn chưa hẳn là dây AB.
Xét ΔOAB, có: AB
⇒ Vậy vào một con đường tròn trung tâm O, nửa đường kính R, (O , R) ta luôn có AB ≤ 2R
3. Quan hệ tình dục vuông góc giữa 2 lần bán kính và dây của mặt đường tròn:
Định lý 2:Quan hệ vuông góc giữa 2 lần bán kính cùng cùng với dây đường tròn được quan niệm như sau: Nếu đường kính mà vuông góc với cùng 1 dây trong một đường tròn thì đi qua trung điểm của dây đó.Chứng minh:
Trường đúng theo 1:Nếu đường kính của đường tròn là CD thì rõ ràng AB sẽ trải qua trung điểm O (tâm) của đường kính CD.
Trường thích hợp 2:Nếu 2 lần bán kính của mặt đường tròn chưa phải là CD
Ta hotline I là giao điểm giữa AB với CD. Lúc ấy ΔOCD tất cả OD = OC = R
⇒ ΔOCD là tam giác cân nặng tại O (Do OC = OD = R)
⇒ Đường cao của ΔOCD là OI và cũng là con đường trung tuyến
⇒ ID = IC (Hay I là trung điểm của CD)
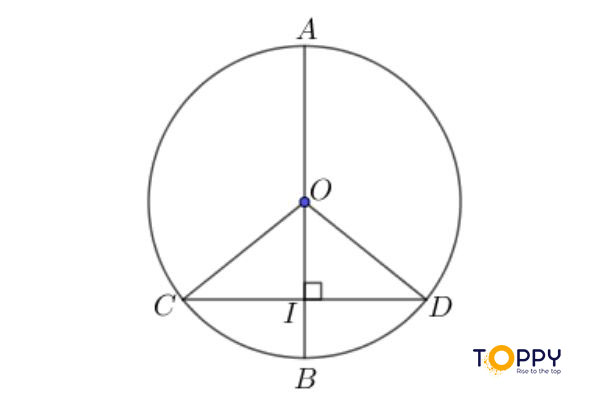
Quan hệ vuông góc giữa 2 lần bán kính và dây của đường tròn
Vậy nếu 2 lần bán kính mà vuông góc với một dây trong một đường tròn thì đi qua trung điểm của dây đó. Đây cũng chính là định lý đặc trưng trong toán 9 đường kính và dây của con đường tròn đề xuất nắm vững.
Định lý 3:Nếu đường kính mà trải qua trung điểm của một dây với không đi qua tâm trong một đường tròn thì vuông góc cùng với dây đó.Xem thêm: Cách Tải Văn Bản Trên Mạng Về Máy Tính, Tải Tệp Xuống
Chứng minh:
Gọi I là giao điểm của đường kính AB cùng dây CD.
⇒ ΔOCD là tam giác cân tại O (Do OC = OD = R)
Mà ta tất cả OI là trung đường của ΔOCD bắt buộc đồng thời cũng là con đường cao của tam giác.
⇒ Vậy OI ⊥ CD trên điểm I.
Đường kính qua trung điểm 1 dây không đi qua tâm đang vuông góc cùng với dây đó
Lưu ý: Trong tình dục vuông góc giữa 2 lần bán kính với dây đường tròn, nếu 2 lần bán kính mà đi qua trung điểm của 1 dây thì có thể sẽ không vuông góc cùng với đó.
Giả sử 2 2 lần bán kính của con đường tròn (O , R) là AB cùng CD.
Khi kia ta bao gồm CD cũng là một trong những dây cung của đường tròn trọng tâm O.
Mà O ∈ CD đồng thời OC = OD (do CD là 2 lần bán kính của con đường tròn chổ chính giữa O)
⇒ O đó là trung điểm của CD.
⇒ khi đó, đường kính AB sẽ đi qua trung điểm O của CD mà lại đường kính sẽ không vuông góc cùng với dây đường tròn.
Lưu ý trong tình dục vuông góc giữa đường kính và dây đường tròn
II. Bài tập 2 lần bán kính và dây của đường tròn sbt:
Trên đó là bài giảng về 2 lần bán kính và dây của đường tròn, nhằm củng vắt lại định hướng của bài học, dưới đấy là một số vấn đề cơ bản về dạng kỹ năng này giúp các em hệ thống hóa lại kiến thức cho quá trình ôn tập tương tự như luyện thi được hiệu quả.
Bài tập 1: (Bài 15/SBT Tập 1, Toán 9, trang 158)
Cho ΔABC, đường cao ông chồng và BH. Chứng tỏ rằng:
B, C, H, K là 4 điểm không thuộc thuộc 1 con đường tròn.HKBài tập 2: (Bài 16/SBT Tập 1, Toán 9, trang 159)
Cho tứ giác ABCD gồm góc B = góc B = 90⁰
Chứng minh A, B, C, D là 4 điểm cùng thuộc trên 1 con đường tròn.So sánh độ lâu năm của cung AB và cung BD. Nếu như AC = BD thì ABCD là tứ giác gì? tại sao?Bài tập 3: (Bài 17/SBT Tập 1, Toán 9, trang 159)
Cho nửa mặt đường tròn (O,AB) (Tâm O, 2 lần bán kính AB) và dây EF không cắt với mặt đường kính. Gọi K cùng I lần lượt là chân đường vuông góc kẻ trường đoản cú B với A mang đến dây EF. Minh chứng IE = KF.
Bài giảng 2 lần bán kính và dây của đường tròn bên trên đã cung cấp kiến thức về lý thuyết cũng tương tự các dạng bài tập cơ bản về bài học này. Hy vọng đây vẫn là đa số thông tin bổ ích dành cho các bạn học sinh và quý phụ huynh có nhu cầu giảng dạy với ôn tập cho con em mình của mình. Đừng quên hay xuyên truy vấn https://pgdngochoi.edu.vn/ để update thêm những kiến thức môn học tập khác nhé!
